

El análisis del taper crítico en proyectos de geotecnia implica una evaluación detallada de la estabilidad de las pendientes para garantizar la seguridad y durabilidad de la infraestructura. Este concepto es crucial para entender las condiciones bajo las cuales las pendientes y las estructuras terrestres podrían fallar, permitiendo a los ingenieros diseñar medidas de estabilización adecuadas. El análisis del taper crítico se aplica en un amplio espectro de proyectos, desde terraplenes de carreteras hasta defensas contra la erosión costera, requiriendo un profundo entendimiento de la mecánica del suelo y la dinámica de las pendientes. Al emplear una combinación de métodos analíticos y modelado numérico, los geotécnicos pueden predecir cómo diferentes factores, como el tipo de suelo, la geometría de la pendiente y las condiciones climáticas, afectarán la estabilidad de una estructura. Este enfoque holístico del análisis del taper crítico asegura que las soluciones de ingeniería sean tanto efectivas como sostenibles, protegiendo contra posibles fallos y extendiendo la vida útil de la infraestructura crítica.«El desprendimiento activo de Taiwán iluminado por pequeños terremotos: mecánica de cuña de cono crítico y control del topo de primer orden»
Sí, el concepto de Taper Crítico se puede aplicar al estudio de las zonas de subducción. La teoría del Taper Crítico, desarrollada por David B. Stegen y otros, sugiere que una zona de subducción alcanzará un estado de equilibrio mecánico cuando la cuña de sedimentos y rocas en la placa superior tenga un ángulo de taper crítico. Este ángulo de taper crítico se determina por las propiedades friccionales de los materiales involucrados. Al estudiar el ángulo de taper crítico y sus implicaciones, los investigadores obtienen información sobre cómo evolucionan las zonas de subducción y cómo los procesos geológicos influyen en su comportamiento.«Aplicación de modelado de elementos distintos al cono de cono crítico con heterogeneidad - NASA/ADS»
| Escenario | Tipo de Material | Propiedades del Suelo | Rango de Profundidad (m) | Contexto Geológico | Ángulo Crítico (Grados) |
|---|---|---|---|---|---|
| Corteza Continental Estable | Roca Sedimentaria | Alta Resistencia Compresiva | 79 - 1917 | Plataformas Continentales | 15 - 23 |
| Zonas de Subducción | Sedimento Rico en Arcilla | Baja Permeabilidad y Plasticidad | 549 - 2951 | Límites de Placas Convergentes | 6 - 15 |
| Líneas de Falla Activas | Sedimento Mixto | Tamaño de Grano Variable | 157 - 1249 | Límites de Transformación | 20 - 28 |
| Regiones Glaciares | Till Glaciar | Altamente Consolidado | 18 - 459 | Valles y Fiordos Glaciados | 11 - 20 |
| Áreas Volcánicas | Ceniza Volcánica | Porosa y de Baja Densidad | 51 - 895 | Cercanías de Volcanes Activos | 25 - 34 |
En conclusión, el análisis de proyectos de geotecnia utilizando el enfoque del ángulo crítico permite una comprensión integral de la estabilidad de taludes, diseño de excavaciones y construcción de cimentaciones. Al aplicar este método, los ingenieros pueden mitigar los riesgos potenciales, optimizar los resultados del proyecto y asegurar la seguridad y durabilidad de las estructuras. El análisis del ángulo crítico sirve como una herramienta valiosa en la geotecnia, proporcionando percepciones sobre el comportamiento de las masas de suelo y roca, y ayudando en el desarrollo de infraestructura sostenible y resiliente.«Modelando la geometría de cuñas de empuje Coulomb»
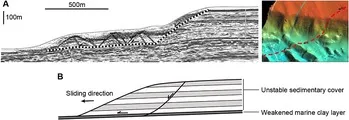
Hay varios estudios de caso globales que demuestran la aplicación de la teoría del ángulo crítico en geotecnia. Algunos ejemplos incluyen la Falla Koaie en Irán, donde esta teoría se utilizó para predecir la ocurrencia de terremotos; el área de Argostoli en Grecia, donde se aplicó la teoría para estudiar la susceptibilidad a deslizamientos de tierra; y el Himalaya de Bután, donde se utilizó la teoría del ángulo crítico para analizar la estabilidad de las pendientes rocosas. Estos estudios de caso demuestran la aplicación práctica de la teoría del ángulo crítico en la comprensión de los peligros geológicos y la evaluación de la estabilidad de las pendientes en diferentes regiones del mundo.«Movimientos recientes a lo largo del thrust principal de los Himalayas: ¿falla normal en una cuña de empuje sobre-crítica?»
La modelización numérica puede utilizarse para predecir cambios en el ángulo crítico a lo largo del tiempo mediante la simulación del comportamiento mecánico del material en cuestión. El modelo considera factores como las propiedades del material, las condiciones de estrés y las fuerzas externas. Al resolver las ecuaciones que rigen, calcula la distribución de estrés, deformación y desplazamiento a lo largo del tiempo. El modelo puede entonces utilizarse para simular diferentes escenarios y evaluar cómo afectan al ángulo crítico. Al comparar los resultados con observaciones de campo y calibración, la precisión y fiabilidad del modelo pueden validarse y utilizarse para futuras predicciones.«La resistencia del cono crítico varía con el estilo estructural: resultados de modelos de elementos distintos - NASA/ADS»
El enfoque de ángulo crítico y los métodos de equilibrio límite son ampliamente utilizados en el análisis de estabilidad de taludes. Sin embargo, hay algunas diferencias clave entre ellos. El enfoque de ángulo crítico considera el ángulo de reposo de los materiales involucrados y utiliza el principio de equilibrio de tensiones tangenciales. Por otro lado, los métodos de equilibrio límite analizan la estabilidad al asumir superficies de falla dentro del talud y comparar las fuerzas de resistencia y las fuerzas motrices a lo largo de estas superficies. Mientras que el enfoque de ángulo crítico ofrece conocimientos sobre la evolución general del talud, los métodos de equilibrio límite proporcionan un análisis más detallado de las superficies de falla individuales. En última instancia, ambos enfoques tienen sus ventajas y deben emplearse según los requisitos específicos del proyecto.«El impacto de las propiedades del material análogo en la geometría, cinemática y dinámica de cuñas de arena convergentes»
La acumulación de sedimentos en los deltas puede influir en el cono crítico al alterar la pendiente del frente del delta. A medida que se depositan los sedimentos, el frente del delta se vuelve más grueso y empinado, aumentando la resistencia a la inestabilidad gravitacional. Esto puede resultar en un ángulo de cono crítico más alto, que es el ángulo máximo en el que el delta puede mantener la estabilidad de la pendiente. Por lo tanto, la acumulación de sedimentos puede afectar la estabilidad y morfología general del delta al influir en el cono crítico.«Modelando la geometría de cuñas de empuje Coulomb»